1.1.3 Factors & Divisors
Factors
Let’s look at the following multiplication: 2 x 3 = 6 —> 2 and 3 are said to be factors of 6.
Factors can also be negative, like in this example: -2 x -3 = 6 —> -2 and -3 are also factors of 6.
From the previous two statements, it seems that the number 6 presumably has 4 factors.
However, the numbers 1 and -1 are factors of every number —>
All the factors of 6 are: {-6, -3, -2, -1, 1, 2, 3, 6}.
Generalizing: The factors of X are those integers which multiplied together equal X.
Divisors
Looking at the previous example, if we took 6 and divided it by one of its factors, the result would be another integer. For example:
- 6 % 2 = 3
- 6 % 3 = 2
This implies that 2 and 3 are divisors of 6 because. In fact, all the factors we found would give an integer if divided by 6.
Generalizing: All the factors of a number are also its divisors.**
**When trying to find the divisors of a number, it might be convenient to find its factors first. Another way of finding the divisors of a number would be to take that number and divide it by all the existing ones less or equal than that number and corroborating which of these give an integer as a result.
Multiples
Multiples are the numbers that result from multiplying a particular number by the integers in the number line that we saw at the beginning.
For example, to find the multiples of 2, we multiply 2 by all the numbers in the integer number line:
2×0 =0, 2×1 = 2, 2×2 = 4, 2×3 = 6, 2×4 = 8, 2x-1 = -2, 2x-2 = -4 … (continues with all the integers)
Hence, the multiples of 2 are {…-4, -2, 0, 2, 4, 6, 8, …}. As we can see, the multiples of a number extend both to -∞ and +∞ in the same way as the integers.
Generalizing: The multiples of a number are the numbers which result from multiplying all the integers (both positive and negative) by that number.
Multiplication Table
With the help of multiples, we can now build a multiplication table. This is a helpful resource to keep in hand and to go through a couple of times.
You should be able to do these multiplications quickly and without much thought.
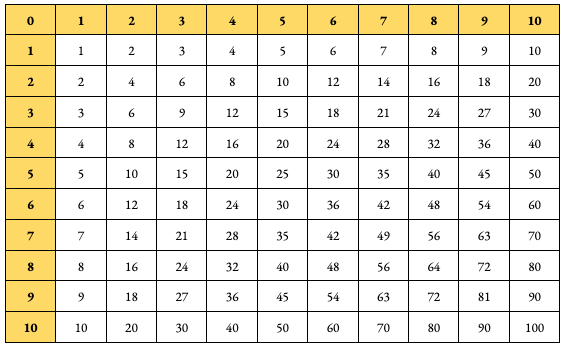
Divisibles
A number is divisible by all of its divisors (factors). Hence, we say a number is divisible by another number when the result of that division is an integer.
For example, 6 is divisible both by 3 and 2 because the result of 6%3 and 6%2 gives 2 and 3, respectively, both integers.
Least Common Multiple (LCM)
The least common multiple of two numbers is simply the least (lowest number) of the multiples common to two numbers. We will only be working with positive integers.
There are also two steps to determine the LCM between 2 numbers.
Example: What is the LCM of 3 and 5?
① Find the positive multiples of 3 and of 5
- Multiples of 3: 3×1 = 3, 3×2= 6, 3×3 = 9, … —> {3, 6, 9, 12, 15, 18, 21…}
- Multiples of 5: 5×1 =5, 5×2= 10, 5×3=15, …—> {5, 10, 15, 20, 25 …}
② What is the lowest common multiple to both 3 and 5? 15. This is your LCM.
Least Common Multiple (LCM) is useful for fraction addition!
For example: 1/3 + 2/5 = (5+3)/15 = 8/15
Where 15 = LCM as we saw before.
(We will look at operations with fractions in the following section, don’t worry!)

Greatest Common Divisor (GCD)
There are also two steps to determine the GCD between 2 numbers.
Example: Determine the GCD of 6 and 15.
① Determine the divisors (factors) of both numbers. In this case, we can think which numbers will give us an integer when dividing our two numbers.***
- Divisors of 6: 1, 2, 3 and 6.
- Divisors of 15: 1, 3, 5 and 15.
***Another approach to find divisors is to find the factors of the numbers mentioned.
② Find the greatest amongst the common ones (in this case, the greatest between 1 and 3): 3.
Two 2-step-strategies!
Use the two 2 step strategies (shown before) to solve LCM and GCD exercises!

Exercises: Factors & Divisors
1, 2, 4 and 8.
The divisors of a number are its factors.
The factors or divisors of 12 are: -12, -6, -4, -3, -2, -1, 1, 2, 3, 4, 6, 12.
(Another way of looking at this is dividing 12 by all the number line integers, both positive and negative, and see which ones yield an integer)
5, 10, 15, 20, 25, 30, …
The factors or divisors of 8 are -8, -4, -2, -1, 1, 2, 4 and 8. Thus, 8 is divisible by these numbers.
Another way is reasoning which numbers will give an integer if acting as a divisor of 8.
Applying the 2-step strategy:
① Find the multiples of 4 and 9.
4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44…
9: 9, 18, 27, 36, 45
② Find the lowest common multiple to both.
LCM = 36.
① Find the divisors (factors) of 14 and 35?
14: 1, 2, 7 and 14.
You can use the strategy of dividing all the integers less or equal than 14 and seeing which produces an integer (you can use a calculator).
35: 1, 5, 7 and 35.
② Find the greatest common divisor to both (the greatest between 1 and 7).
GCM = 7.
