1.1.6 Prime Numbers & Prime Factors
Prime Numbers
A prime number is by definition a number which is only divided by 1 and itself. The list of the first 10 prime numbers is: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29…}. If a number is not a prime number, it is called a composite number.
Prime Factors
As we recall from the topic of factors: “the factors of X are those integers which multiplied together equal X”. For example, the factors of 6 are 1, 2, 3 and 6 because any right combination of these numbers gives us 6.
But what if we only want to have prime numbers as factors?
In that case, the previous factor list would reduce from 1, 2, 3 and 6 to simply 2 and 3, given that 1 and 6 are NOT prime numbers.
In general, we can express a number only as a multiplication of its prime numbers. Enter, prime factorization.
Why is this even useful?
The usefulness of this type of factorization entails finding a multiplication in its simplest form to express another number. In this sense, prime numbers guarantee the simplest component to this expression because prime numbers can’t be further simplified.
Example 1: Factorize 18.
18 = 2 x 9 (Normal Factorization)
18 = 2 x 3 x 3 (Prime Factorization)
As we can see from both factorizations, the normal factorization can be further simplified by expressing 9 in terms of prime numbers (as 3 times 3). Whereas the prime factorization can’t be further simplified and it represents the “leanest” version of a factorization.
Prime Factorization
As we already discussed, the use of prime numbers in factorization is that they can’t be further simplified
Example 1: Factorize 27 using prime numbers.
27 = 3 x 3 x 3 = 3 ^ 3
Convention: When we use ^ we are representing an exponent (we’ll see it in section 3). For example, 5^2 means 5×5 and 3^3 means 3x3x3.
Now we will solve other factorizations that aren’t so easy by applying the Line Method.
Technique: The Line Method
We’ll explain this technique through an example.
Example: Find the prime factorization of 32.
① Grab a piece of paper. Write down your number (32), then draw a straight vertical line next to your number.
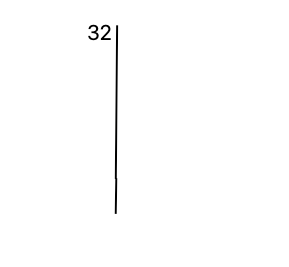
② Which is the biggest prime number that is also a divisor of your number?
Looking at the list of prime numbers above, we quickly realize that all the numbers bigger than 2 are not divisors. Thus, our biggest prime divisor is 2. Write down 2 next to 32.
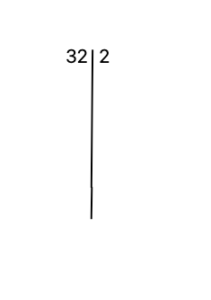
③ Below your number, compute the division between those two numbers. In our case: 32%2 = 16. Then write that number down on the left column.
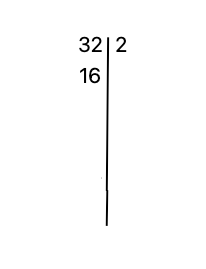
④ Repeat the process with the new resulting number from the division.
Repeating step 1, we find that the biggest prime divisor of 16 is 2 again. Thus, we write down 2 next to our number.
Below 16, we compute the division 16%2 = 8.
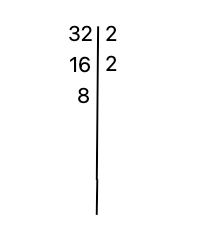
⑤ Keep repeating until you can’t factorize any further because the number on the left column is 1.
The next steps to find the prime divisors are:
- (8 on left column) Biggest prime divisor of 8: 2 —> 8 % 2 = 4
- (4 on left column) Biggest prime divisor of 4: 2 —> 4 % 2 = 2
- (2 on left column) Biggest prime divisor of 2: 2 —> 2 % 2 = 1
After fully factoring, the final drawing will look like this. (Notice that 1 can’t be factored any further)
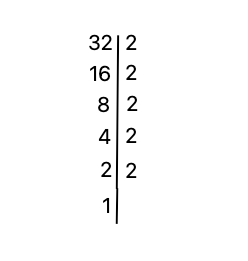
⑥ The numbers on the right column are our prime factors. We now need to multiply them together.
Answer: 32 = 2 x 2 x 2 x 2 x 2 = 2^5 (Prime factorization of 32)
Use the Line Method!
It’s effective and quick and even some engineers use it!

Exercises: Prime Numbers & Prime Factorization
Following the Line Method steps:
1) 35 |
2) Biggest prime divisor of 35: 7
35 | 7
5 |
3) Biggest prime divisor of 5: 5
35 | 7
5 | 5
1 |
4) 1 is a prime number so this is where we stop.
5) Multiplying the divisors together:
Answer: 35 = 7 x 5 = 5 x 7 (it’s convenient to write it down in ascending order)
Following the Line Method steps:
1) 72 |
2) We could try to find a bigger prime number, or we could start dividing by 2.
72 | 2
36
3) Again, we use 2 until we reduce the left side number to a prime or a divisible by a greater number, like 3.
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 |
Answer: 72 = 2 x 2 x 2 x 3 x 3 = (2^3)(3^2)

