1.1.2 Basic Arithmetic Operations
Properties of Addition
Rule 1. Commutative: A + B = B + A
Rule 2. Associative: A + (B+C) = (A+B) + C
Rule 3. Identity: A = B —> A + C = B + C.
Properties of Subtraction
A subtraction is basically an addition, except one of the numbers we’re adding has a negative sign.
For example, 4 – 2 could be seen as 4 + (-2). This last expression is an addition with a negative number (-2).
Thus, all of the properties we saw for addition apply also to subtraction
Properties of Multiplication
The first three properties are the same as in addition:
Rule 1. Commutative: A x B = B x A
Rule 2. Associative: A x (B x C) = (A x B) x C
Rule 3. Identity: A x 1 = A
And then there are two new properties, exclusive to multiplication:
Rule 4. Distributive: A x (B – C) = A x B – A x C *
Rule 5. Zero: A x 0 = 0
*This property will be very important in Algebra
Parenthesis = (Multiplication)
Besides using the multiplication sign (x) we can use parentheses in order to express a multiplication – ().
Example 1: (3)(3) = 3 x 3 = 9
Most times, parentheses are used to separate terms (additions) or negative numbers.
Example 2: (4+5)(-3) = (9)(-3) = -27
Properties of Division
In the same way as we saw that a subtraction can be seen as an addition, we can think of a division as a multiplication of the reciprocal number (one over that number).
For example, 2 % 4 can be seen as 2 x (1/4), 1/4 being the reciprocal of 4.
Therefore, all the properties we saw for multiplication apply also to division. We need to make an important comment about the Zero property:
Rule 5. Dividing a number by zero is never allowed.
Order of Operations
When doing several arithmetic operations at the same time, you need to respect the following order:
① Multiplying and dividing
② Adding and subtracting
Example: 5 x 2 + 9 % 3
Respecting the order above, we first divide (9%3 = 3) and multiply (5 x 2 = 10), and then we perform the addition (3 + 10 = 13).
Notice that if we were to have used another order, we would have obtained a different (incorrect) result. For example, if we had added first (2 + 9 = 11), then multiplied (5 x 11 = 55) and finally divided (55 % 3 = 18.3); we would have obtained 18.3 ≠ 13.
Terms
Before we even start talking about algebra, we need to mention the existence of terms in a mathematical expression.
Terms are simply the elements that are being added or subtracted within the mathematical expression.
Example 1: 5 + 2 (1st term = 5, 2nd term = 2)
Example 2: 5 – 3 + 2 (1st term = 5, 2nd term = -3, 3rd term = 2)
If there is a multiplication in the expression, we don’t say that each member of the multiplication is a term on its own but rather we identify it as a coefficient.
Example 1: 5a (which means 5 x a) + 2. Imagine that a is a variable which can represent any number.
1st term = 5a, 2nd term = 2 and 5 is the coefficient of a.
Example 2: -3b (means -3 x b) -2 + 4a. Imagine that a and b are variables which can represent any number.
1st term = -3b, 2nd term = -2, 3rd term = 4a, -3 is the coefficient of b and 4 is the coefficient of a.
Sign Multiplication
The following convention applies for the multiplication (and division) of signs:
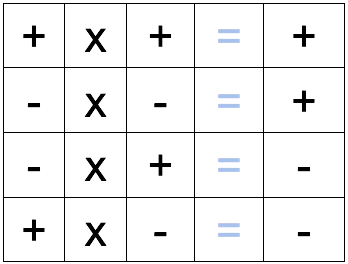
A trick to memorize the sign table

